画像をダウンロード 2^n-1 formula 250859-S=n(n+1)/2 formula

SOLUTION 1/21/41/81/2^n=11/2^n prove by mathematical induction that above statement holds true for every integer n belongs to N HINTto prove that 11/2^ (k1) Question 1/21/41/81/2^n=11/2^n You can put this solution on YOUR website!I have wondered how the closed form for the sum of squares for the first n natural numbers was derived Given the formula for the sum 1^22^2n^2= n(n1)(2n1)/6 I learned to prove its correctness using mathematical induction However, I neverInductive Step to prove is 2 n 1 = 2 n 2 − 1 Our hypothesis is 2 n = 2 n 1 − 1 Here is where I'm getting off track Lets look at the right side of the last equation 2 n 1 − 1 I can rewrite this as the following 2 1 ( 2 n) − 1 But, from our hypothesis 2 n = 2 n 1 − 1 Thus

Solved Just Need Help Finding The A 3 N General Formula Chegg Com

S=n(n+1)/2 formula

S=n(n+1)/2 formula-When n = 1 the left side has only one term, 2 n1 = 2 11 = 2 0 = 1 The right side is 2 n 1= 2 1 1 = 1 Thus the statement is true for n = 1 The second step is the inductive step You need to show that if the statement is true for any particular value of n it is also true for the next value of n If you can do this then, since it is true= 1×2×3×4××n For n=0, 0!

Prove By Mathematical Induction 3 4 5 N 2 N N Homeworklib

You can square a number in Excel with the power function, which is represented by the carat ^ symbolUse the formula =N^2, in which N is either a number or the value of the cell you want to squareThis formula can be used multiple times throughout a worksheet Square a• Mathematical induction is valid because of the well ordering property • Proof –Suppose that P(1) holds and P(k) →P(k 1) is true for all positive integers k –Assume there is at least one positive integer n for which P(n) is false Then the set S of positive integers for which P(n) is false is nonempty –By the wellordering property, S has a least element, say mThe i does not appear in the formula so all the terms are the same 2 T(n) = n (n1) T(n) = n (n1) / 2

Jun 27, 17 · #"using the method of "color(blue)"proof by induction"# #"this involves the following steps "# #• " prove true for some value, say n = 1"# #• " assume the result is true for n = k"#If 2 n1 is prime, then so is n The goal of this short "footnote" is to prove the following theorem used in the discussion of Mersenne primes Theorem If for some positive integer n, 2 n1 is prime, then so is n ProofMay 31, 18 · In this section we will discuss using the Ratio Test to determine if an infinite series converges absolutely or diverges The Ratio Test can be used on any series, but unfortunately will not always yield a conclusive answer as to whether a series will converge absolutely or diverge A proof of the Ratio Test is also given

And calculated by the product of integer numbers from 1 to n For n>0, n!Tulip® Fabric Dye 2N1 Formula Black $349 Best Sellers OneStep TieDye Kit Ice Cream Shoppe $1499 Dimensional Fabric Paint Mini Writers 30 Pack $1699 TieDye Party Kit $2999 Fabric Dyes Tulip® Fabric Dye 2N1 Formula Black Add Your Review $349 Tulip® Permanent Fabric Dye is your classically easy solution for onecolor dyeingNov 24, 08 · I'm afraid your answer is incomplete, so allow me to generate examples 1) 2^n = 8 To solve an equation like this, as long as you recognize that the right hand side is

How To Prove A Formula For The Sum Of Powers Of 2 By Induction Mathematics Stack Exchange

Prove By Induction Sum Of The First N Cubes 1 3 2 3 3 3 N 3 Youtube

Note this common technique In the "n = k 1" step, it is usually a good first step to write out the whole formula in terms of k 1, and then break off the "n = k" part, so you can replace it with whatever assumption you made about n = k in the previous stepFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorAsher began working through the problem using the steps His work is shown 1 Write the formula V = lwh 2 Substitute for the known values 210 = l( 3)(5) A prism has a length of l, width of 3 feet, and height of 5 feet A prism has a width of 3 feet, a height of 5 feet, and a volume of 210 ft3

Fibonacci Mathematics A First Generalization

Prove That X 2n 1 Y 2n 1 Is Divisible By X Y For All N Belongs To N Mathematics Topperlearning Com C47jvkww

Oct 09, 12 · You need to use reduction formula to integrate the function, such that `int sec^n x dx = int sec^(n2) x* sec^2 x dx` You need to use integration by parts, such thatJul 12, 12 · n is not prime (aka n is composite) ==> 2^n 1 is composite Assume n is composite Let n = p*q, where neither p nor q are 1 Then, 2^n 1 = (2^p)^q 1 = (2^p 1)*((2^p)^(q1) (2^p)^(q2) (2^p) 1) Note that 2^p 1 > 1 Also, ((2^p)^(q1) (2^p)^(q2) (2^p) 1) > 1 So we have factored 2^n 1, thus it is not prime(2n 1)(2n 3) 5x3x1 / (n!) 2 = 2 n (2n 1)(2n 3) 5x3x1 / (n!) = 2 n 1x3x5 (2n 3)(2n 1) / (n!)

Gamma Function Wikipedia

Proof Of 1 2 2 2 Cdots N 2 N 3 3 N 2 2 N 6 Mathematics Stack Exchange

Theorem The sum of the first n powers of two is 2n – 1 Proof By inductionLet P(n) be "the sum of the first n powers of two is 2n – 1" We will show P(n) is true for all n ∈ ℕ For our base case, we need to show P(0) is true, meaning the sum of the first zero powers of two is – 1 Since the sum of the first zero powers of two is 0 = – 1, we see= 1 Factorial definition formulaFrequently Asked Questions How do you find the sum of square numbers?

Tulip Fabric Dye 2 N 1 Formula Aqua Tulip Color

Using Sum Of Squares Triangle To Prove Sum Of Squares Formula Mtg My Triangle Geometry

Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyDec 29, 09 · = (1/4)n^2(n 1)^2 Now, you can verify the expression using induction Notice that this method, without proving that every sum of polynomial expressions is a polynomial of at most one degree larger than the summed polynomials, cannot actually prove that the expression is correct for all nSection 2 The Principle of Induction 9 Step b) (the inductive step) we assume it is true for n = k, ie, assume Xk j=1 (2j −1) = k2 and need to show that it follows that

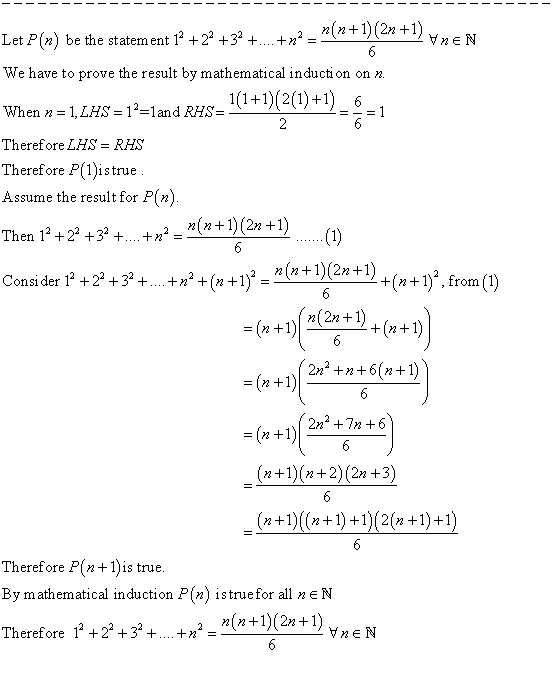
Show That N N 1 2n 1 Is Divisible By 6 So That The Formula

The Wallis Product Formula For Pi And Its Proof Mind Your Decisions

May 19, 18 · I_n = int \ sec^nx \ dx => I_n = 1/(n1)tanx \ sec^(n2)x (n2)/(n1)I_(n2) J_n = int \ tan^nx \ dx => J_n = tan^(n1)x/(n1) J_(n2) We seek reduction formula for A) I_n = \ int \ sec^nx \ dx B) J_n = \ int \ tan^nx \ dx Part (A) If we assume that n gt 2, We can write I_n = \ int \ sec^(n2)x \ sec^2x \ dx We can then apply Integration By PartsMay 09, 19 · In this section we will discuss using the Comparison Test and Limit Comparison Tests to determine if an infinite series converges or diverges In order to use either test the terms of the infinite series must be positive Proofs for both tests are also givenThe sum of the first n squares, 1 2 2 2 n 2 = n(n1)(2n1)/6 For example, 1 2 2 2 10 2 =10×11×21/6=385 This result is usually proved by a method known as mathematical induction, and whereas it is a useful method for showing that a formula is true, it does not offer any insight into where the formula

The Taylor Formula Prezentaciya Onlajn

Engineering Formula Sheet Formulae Engineering Formula Sheet Cea 6 X O 2 N 1 Sample 1 5b Pdf Document

Weiman Granite Cleaner Polish and Protect 3 in 1 2 Pack StreakFree, pH Neutral Formula for Daily Use on Interior and Exterior Natural Stone 24 Fl Oz (Pack of 2) 46 out of 5 stars 1,077 $1698 $ 16 98 ($035/FL Oz) Save more with Subscribe & Save Get it as soon as Mon, Apr 19Dec 29,  · Using our new terminology, we can state that the series \( \sum\limits_{n=1}^\infty 1/2^n\) converges, and \( \sum\limits_{n=1}^\infty 1/2^n = 1\) We will explore a variety of series in this section We start with two series that diverge, showing how we might discern divergence3 Find and prove by induction a formula for P n i=1 (2i 1) (ie, the sum of the rst n odd numbers), where n 2Z Proof We will prove by induction that, for all n 2Z , (1) i=1 (2i 1) = n2 Base case When n = 1, the left side of (1) is 1, and the right side is 12 = 1, so both sides are equal and (1) is true for n = 1 Induction step Let k 2Z

The Catalan Numbers And Their Applications 1 2

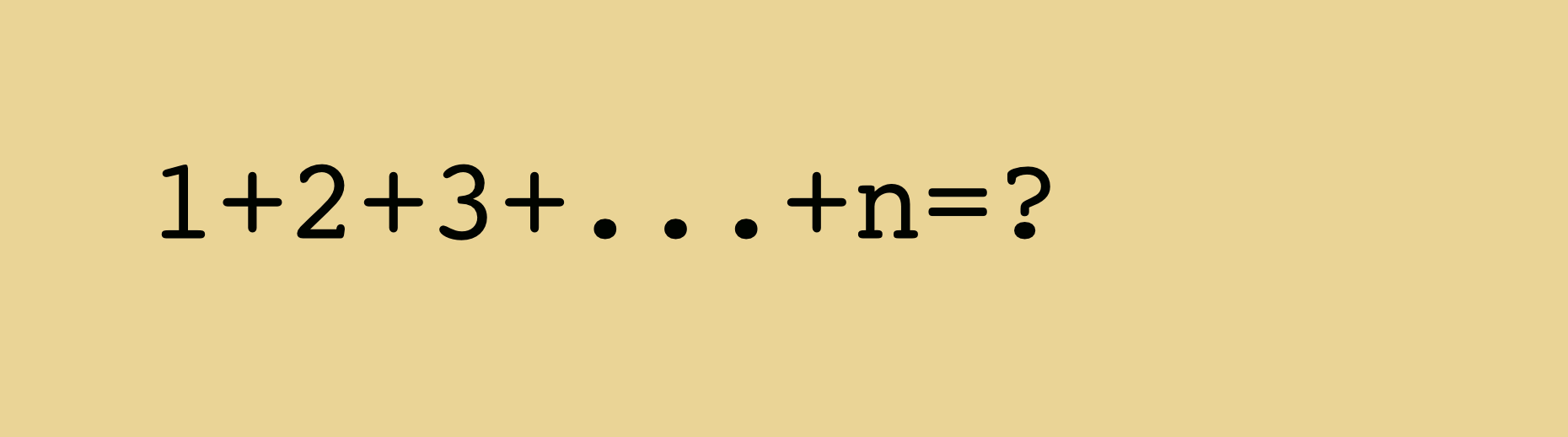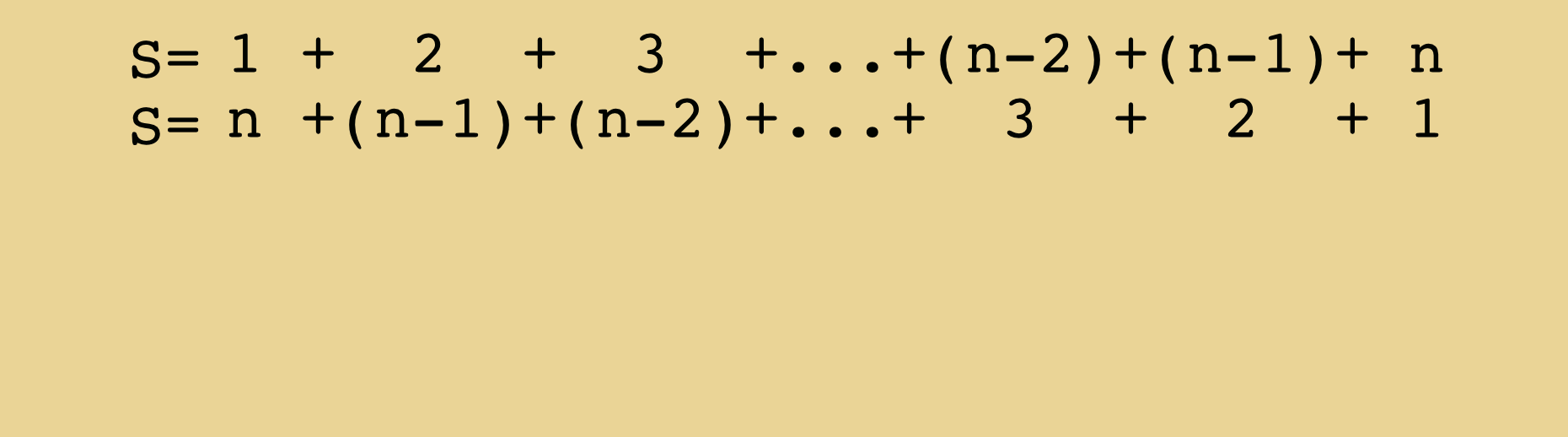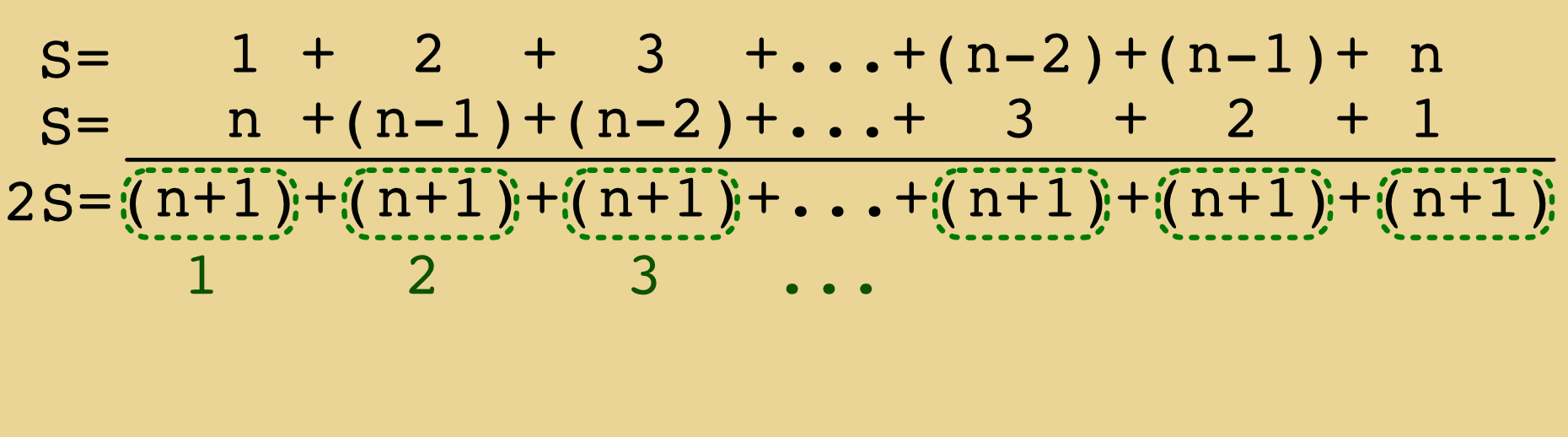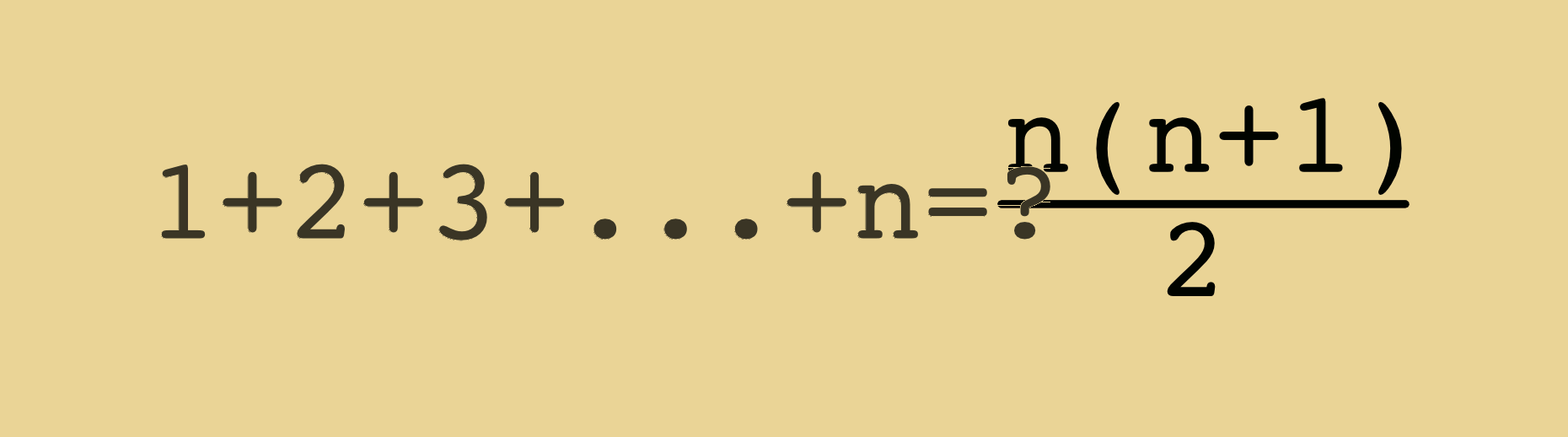
File Animated Proof For The Formula Giving The Sum Of The First Integers 1 2 N Gif Wikimedia Commons

Formula for the sum 1 2 2 2 3 2 ⋯ n 2 1^2 2^2 3^2 \cdots n^2 1 2 2 2 3 2 ⋯ n 2 Suppose we have the following sum S n = 1 2 2 2 3 2 ⋯ n 2 = ∑ i = 1 n i 2Solving 2n 2n1 = 0 directly Earlier we factored this polynomial by splitting the middle term let us now solve the equation by Completing The Square and by using the Quadratic Formula Parabola, Finding the Vertex 41 Find the Vertex of y = 2n 2n1 Parabolas have a highest or a lowest point called the VertexGeometric Progression is a type of sequence where each successive term is the result of multiplying a constant number to its preceding term Learn more about the formula of nth term, sum of GP with examples at BYJU'S

Is There Any Elementary Formula For The Sequence Sum K 1 N Left 2k 1 Right Left Frac 1 2 Right K Mathematics Stack Exchange

Therom 1 8 2 N Choose K N Choose N K N Choose K N 1 Choose K Homeworklib

17 Answers Nihar Tiwari , B E from Shri Govindram Seksaria Institute of Technology and Science () Answered 3 years ago As I know the formula for adding 1,2,3n is given by n (n1)/2 Comparing to above formula if we want to calculate sum up to n1 , using the above formula we get n1 (n11)/2 That is n (n1)/2Factorial (n!) The factorial of n is denoted by n!= 2xn ( 2n 1) 2 ( n 1) 2x232x11 / (n!) 2 = 2 n n(n 1)(n 2)(n 3) 3 x2 x1(2n 1)(2n 3) 5x3x1 / (n!) 2 = 2 n n!

Finding Proof For The Single Direction Paper Folding Theorem Mathhelp

Pdf Formulas For Pi N And The N Th Prime

Two sample induction problems 1 Find a formula for 1 4 7 (3n 2) for positive integers n, and then verify your formula by mathematical inductionThat means that the total number of compare/swaps you have to do is (n 1) (n 2) This is an arithmetic series, and the equation for the total number of times is (n 1)*n / 2 Example if the size of the list is N = 5, then you do 4 3 2 1 = 10 swaps and notice that 10Induction Examples Question 7 Consider the famous Fibonacci sequence fxng1 n=1, de ned by the relations x1 = 1, x2 = 1, and xn = xn 1 xn 2 for n 3 (a) Compute x (b) Use an extended Principle of Mathematical Induction in order to show that for n 1, xn = 1

Answered I Proving A Formula Use Mathematical Bartleby

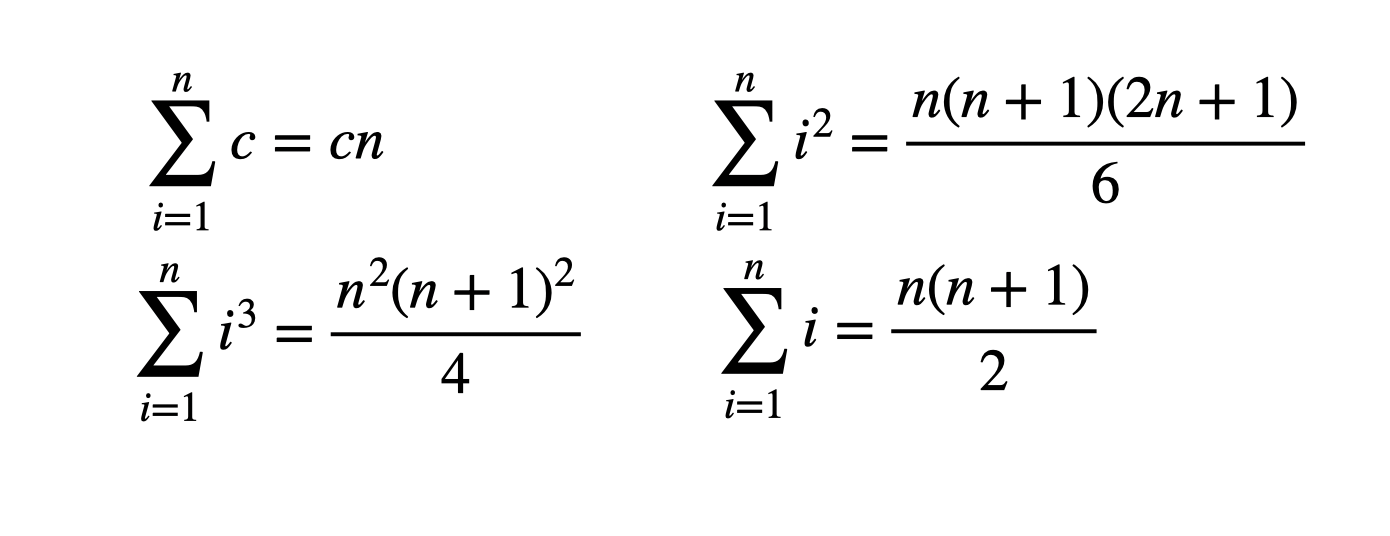
I Can T Derive These Summation Formulas So I Ll Just Model Them In Python By Rhett Allain The Startup Medium

Buy Vitamin D3 5000IU Plus K2, 2 in 1 Formula, Vitamin D3 Liquid with Vitamin K2, 300 SoftGels, Immune Vitamin Complex, Support Your Heart, Teeth, Joint Health and Immune Function, No GMO on Amazoncom FREE SHIPPING on qualified ordersN = a2 n 1 a n 2 No This is not linear because of a2 n 1 f a n = a n 2 Yes Degree 2 g a n = a n 1 n No This is nonhomogeneous because of the n 2 ICS 241 Discrete Mathematics II (Spring 15) pg 524 # 3 Solve these recurrence relations together with the initial conditions given a a n = 2aApr 12, 21 · A naive approach is to calculate the sum is to add every power of 2 form 0 to n Below is the implementation of above approach

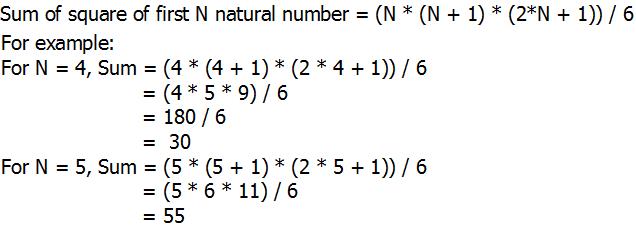
Python Program For Sum Of Squares Of First N Natural Numbers Geeksforgeeks

Mathematical Induction Induction Is The Most Important Proof

Solve Quadratic Equation using the Quadratic Formula 53 Solving n 2 n30 = 0 by the Quadratic Formula According to the Quadratic Formula, n , the solution for An 2 BnC = 0 , where A, B and C are numbers, often called coefficients, is given by

1234n Formula

Tie Dye Your Summer Tulip Fabric Dye 2 N 1 Formula Bright Pink

What Is The Rydberg Formula And How Does It Work

Proof By Induction Wolfram Demonstrations Project

n2 Formula Proof

Solved Let E N 1 N 1 N Follow The Following Proced Chegg Com

Lot Of 2 Eucerin Aquaphor Gentle Wash Shampoo 2 N 1 Formula Ebay

If For A Positive Integer N The Quadratic Equation X X 1 X 1 X 2 N 1 X X N 10n Has Two Consecutive Integral Solutions Then N Is Equal To Xznu4cee Mathematics Topperlearning Com

Fm Series Ppt Download

Wallis Formula And Stirling Formula In The Program Programmer Sought

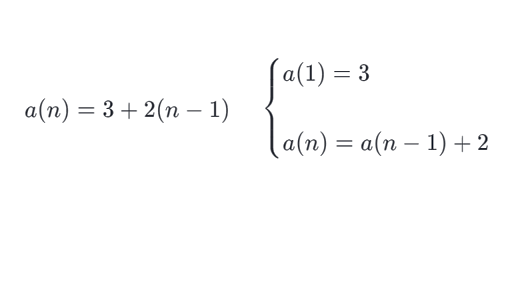
Intro To Arithmetic Sequence Formulas Algebra Article Khan Academy

Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf

Answered Use Mathematical Induction To Prove The Bartleby

Solved Just Need Help Finding The A 3 N General Formula Chegg Com

Formulas N N 1 K 1

Buy Skin Formulas Mask Exfoliator Shop Online At Eyrebrushed Ie

Is This Modern Programming Interview Challenge S Solution Unreliable Stack Overflow

Prove By Mathematical Induction 3 4 5 N 2 N N Homeworklib

Formula 1 2 3 4

A In The Formula S N N 2 2a N 1 D Make D As The Subje

Ex 5 3 9 If Sum Of First 7 Terms Of An Ap Is 49 And 17 Term Is 2

James Tanton على تويتر What S The Next Number In The Sequence 2 4 6 8 Write A Formula That Gives 2 For N 1 4 For N 2 6 For N 3 8 For

Stirling Numbers Of The Second Kind Wikipedia

Tie Dye Your Summer Tulip Fabric Dye 2 N 1 Formula Black

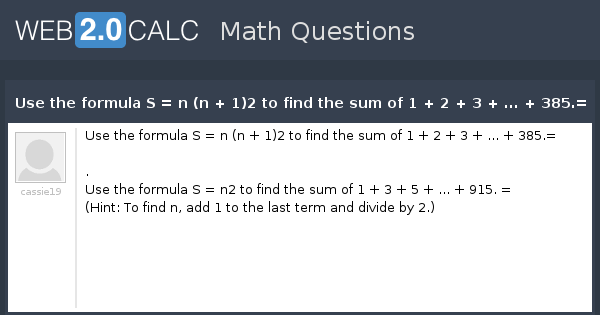
View Question Use The Formula S N N 1 2 To Find The Sum Of 1 2 3 385

Faulhaber S Formula Wikipedia

Ex 7 4 2 Determine N If I 2nc3 Nc3 12 1 Chapter 7

Math 1210 Solutions To Assignment 1 Fall 12 1 A Use

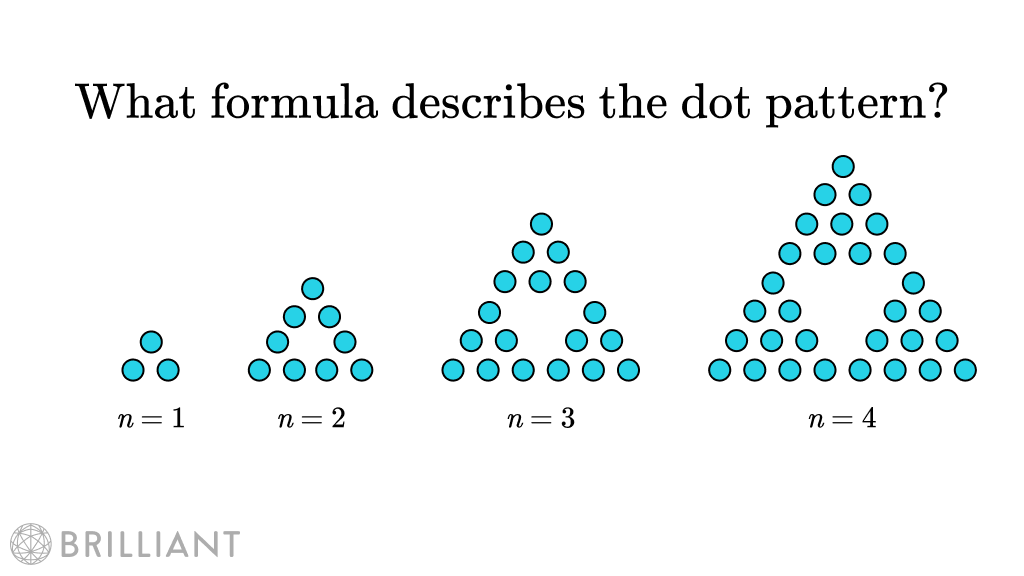
Brilliant Org Which Formula Describes The Number Of Dots In This Pattern A 3 2n 1 B 3n N 1 2 C 3 N D 3 6 N 1

Skin Formulas Mask Exfoliator 2n1 Formula Elegance Beauty

Solved In Exercises 5 18 Use Mathematical Induction To P Chegg Com

Find The Sum Of N Terms Of The Series 1 2 4 1 4 6

Blog Page 168 Of 173 Stumbling Robot

What Is The Explicit Formula For This Geometric Sequence 8 4 2 1 A A N 1 2 8 N 1 B Brainly Com

5 3 Geometric Sequences And Sums

Sum Of N 2 Page 1 Line 17qq Com

5 4 Mathematical Induction T

Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy

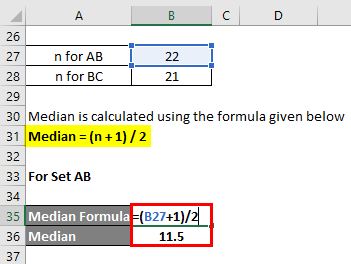
Median Formula How To Calculate Median Calculator Excel Template

Asymptotic Approximations And Inclusions Of The Bernoulli Numbers

n2 Formula

A Short Explanation Of Le Mystere D Urbicande Francois Schuiten Benoit Peeters

Pdf Important Sum Formulas Omid Motahed Academia Edu

How To 12 Proof By Induction 1 3 2 3 3 3 N 3 N N 1 2 2 N 2 N 1 2 4 Prove Mathgotserved Youtube

Important Formulas In Combinatorics Mathoverflow

What Will Be Series Of 2n Sum Formula Quora

Solved 6 10 Points Integer N 2 1 Let P N Following Equation N 1 2 N2n 2 2 1 N 1 22 1 2 2 22 3 23 Q

Answered And N 2n 1 N 1 3 5 13 The Bartleby

Proof By Induction Wolfram Demonstrations Project

2pts Which Formula Defines See How To Solve It At Qanda

Tulip Fabric Dye 2 N 1 Formula Turquoise Tulip Color

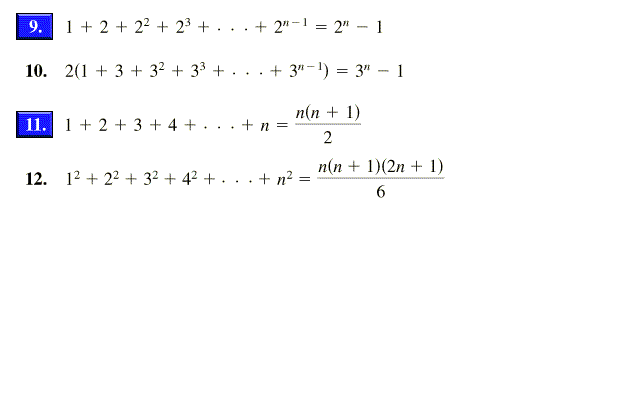
Solved In Exercises 5 18 Use Mathematical Induction To P Chegg Com

4 1 Higher Order Derivatives

Mathematical Induction Recursion Ppt Download

N N 1 2x 3x2 N 1 X R X 1 1 1 N 1 N 1 1 X 22 N 1 1 X 23 1 N 1 N 1 1 X 24 N 1 1 X 2 Maths Principle Of Mathematical Induction Meritnation Com

Pdf A P Adic Formula For The N Orlund Numbers And For Bernoulli Numbers Of The Second Kind

N Formula For Voltage Drop Calculation Of Voltage Drop Vd

Sum Of The Series 2 2 4 2 4 6 2 4 6 8 2 4 6 8 2n Geeksforgeeks

Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot

What Does S Stand For In The Formula S N 2a N 1 D 2 Quora

Untitled Document

How To Derive N 1 2 From 1 2 3 N N Quora

Sum Of Squares Of Odd Numbers 1 2 3 2 5 2 2n 1 2 Derivation Formula Prmo Rmo Iit Youtube

Sum Of N Natural Numbers Formula Page 1 Line 17qq Com

Incoming Term: 2^n-1 formula, 1+2+3+...+(n-1) formula, 2^0+2^1+...+2^n-1 formula, (x^2+1)^n reduction formula, n(n+1)/2 formula proof, s=n(n+1)/2 formula, 1*2*3*...*n formula matematica, 2^n formula, is 2^(n+1) = o(2^n),